Profit Maximization Definition
Profit maximization can be defined as a process in the long run or short run to identify the most efficient manner to increase profits.
It is mainly concerned with the determination of price and output level that returns the maximum profit. It is an important assumption that helped economists in the formulation of various economic theories, such as price and production theories.
Table of Content
Profit Maximisation Formula
According to conventional economists, profit maximization is the only objective of organisations, making it as the base of conventional theories. It is also regarded as the most reasonable and productive business objective of an organisation.
In addition, profit maximization helps in determining the behaviour of business organisations and effect of various economic factors, such as price and output, in different market conditions.
The total profit (Π) of a business organisation is calculated by taking the difference between Total Revenue (TR) and Total Cost (TC). Thus,
Π =TR- TC
Profit is maximum when the difference between the total revenue and total cost is maximum.
For profit maximization, two conditions must be fulfilled, namely, the
First Order Condition
Under first order condition, Marginal Revenue (MR) should be equal to Marginal Cost (MC).
Marginal revenue can be defined as the revenue generated from sale of the last unit of output, on the other hand, marginal cost can be described as the cost incurred in the production of one additional unit of output. Both TR and TC functions involve a common variable, which is output level (Q).
The first order condition states that the first derivative of profit must be equal to zero.
We know Π =TR- TC
Taking its derivative with respect to Q,
∂Π / ∂Q = ∂TR/ ∂Q -∂TC/ ∂Q= 0
This condition holds only when ∂TR/ ∂Q = ∂TC/ ∂Q
∂TR/ ∂Q provides the slope of the TR curve, which, in turn, gives MR. On the other hand, ∂TC/ ∂Q gives the slope of the TC curve, which is the same as MC. Thus, the first-order condition for profit maximisation
is MR=MC.
Second Order Condition
Second order condition requires that the first order condition must be satisfied in case of decreasing MR and rising MC. This condition is shown in Figure 1:
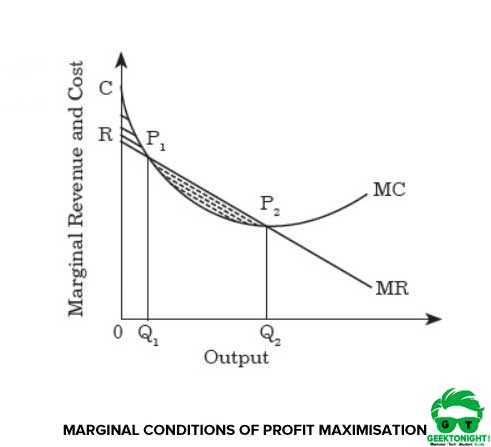
As shown in Figure 1, MR and MC curves are derived from TR and TC functions. It can also be observed from Figure 1 that MR and MC curves intersect at points P1 and P2. At point P2, MR is less than MC, thus, the second order condition is satisfied at point P2. Numerically, the second order condition is given as:
∂2Π / ∂Q2 = ∂2TR/ ∂Q2 — ∂2TC/ ∂Q2
∂2TR/ ∂Q2 — ∂2TC/ ∂Q2 < 0
∂2TR/ ∂Q2 < ∂2TC/ ∂Q2
Slope of MR < Slope of MC
From the aforementioned equation, it can be concluded that MC must have a steeper slope than MR or MC must intersect from below. Thus, profit is maximised when both the first and second order conditions are satisfied.
As mentioned, profit maximisation happens both in the short run as well as long run. Let us study about both the cases in the subsequent sections.
Profit Maximisation in Short Run
Short run can be defined as a time period in which at least one input is fixed. However, the period of time that can be considered as the short run is completely dependent on the industry’s characteristics.
For example, service industries can attain profit in two weeks after operations. In this case, two weeks can be considered as short run. In the short run, profit maximisation occurs in different types of market structures (perfect competition and imperfect competition).
Let us study about the profit maximisation in these two market structures:
Under Perfect Competition
As discussed earlier, under perfect competition, a large number of buyers exist producing the same products.
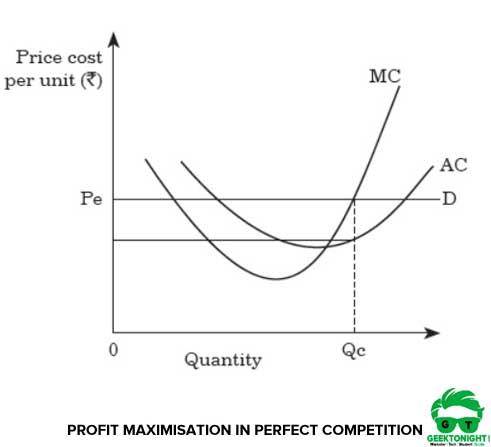
Thus, the profit-maximising output is determined at the point where extra revenue obtained by selling the last unit becomes equal to the marginal cost incurred in the production of that unit. Figure 2 shows the profit maximisation under perfect competition:
In Figure 2, D is the demand curve and the condition of profit maximisation is satisfied at the point Qc, where price equals marginal cost. If the quantity to be produced is increased by the organisation, the marginal revenue Pe becomes less than the marginal costs, as shown by the curve MC. This in turn decreases the profits.
Thus, Qc is the short run equilibrium point, where MR = MC. Therefore, the organisation needs to produce an output level of Qc in order to maximise its profit under perfect competition.
Under Imperfect Competition
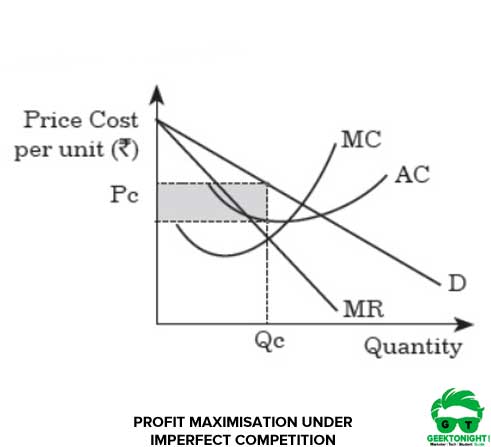
Under imperfect competition, organisations are responsible for determining the profit maximising rate of output levels and price. The demand, marginal revenue and cost curves for a profit maximising organisation under imperfect competition is shown in Figure 3:
In Figure 3, it can be seen that at point Qc, the profit of the organisation is maximised. At Qc, the corresponding price is Pc as shown by the demand curve D.
Thus, at the quantity produced Qc, marginal revenue becomes equal to marginal cost, i.e., MR = MC. The profit earned by the organisation is depicted by the shaded area.
Profit Maximisation in Long Run
Long run can be described as the time period in which all the inputs are variable. Similar to profit maximisation in the short run, organisations maximise profits under perfect competition and imperfect competition. Let us study about the profit maximisation in these two market structures:
Under Perfect Competition
As mentioned, in the long run, all inputs are variable. Similar to short run, in the long run, an organisation must satisfy the condition of MR = MC to maximise its profit. Figure 4 shows the profit maximisation of an organisation under perfect competition:
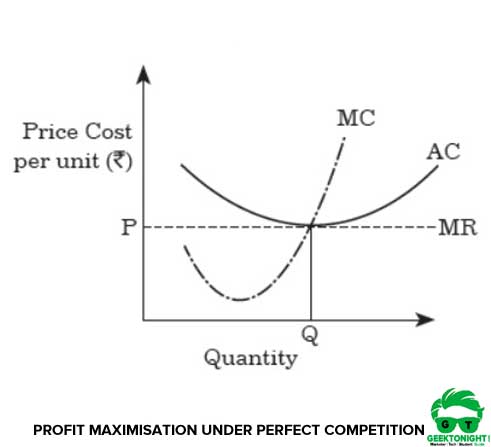
In Figure 4, the profit maximising level of output, where marginal cost equals marginal revenue, results in an equilibrium quantity of Q units of output. Thus, the equilibrium point at which the organisation maximises its profit in perfect competition is at the output rate Q.
Under Imperfect Competition
In the long run, the profits are similar to the way generated in perfect competition. Therefore, an organisation maximises its profit by equalising its marginal revenue and marginal costs. Figure 5 shows the profit maximisation of an organisation under imperfect competition:
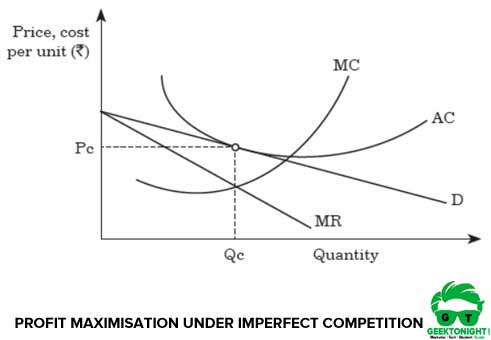
From Figure 5, it can be concluded that to maximise its profit the organisation must produce the quantity Qc units at the price Pc. Also, in Figure 5, demand curve is tangent to average cost equalising price and average cost at Pc and Qc.
Thus, there is no scope of economic profits for other firms, restricting their entries in the markets. Therefore, Pc and Qc are the equilibrium points for the organisations for a long period of time in imperfect competition.
Also Read: What is Demand Forecasting?
Business Economics Tutorial
(Click on Topic to Read)
Go On, Share article with Friends
Did we miss something in Business Economics Tutorial? Come on! Tell us what you think about our article on Profit Maximisation | Business Economics in the comments section.
Business Economics Tutorial
(Click on Topic to Read)