Types of Price Elasticity of Demand
There are 5 types of price elasticity of demand, mentioned in the figure below:
- Perfectly Elastic Demand
- Perfectly Inelastic Demand
- Relatively Elastic Demand
- Relatively Inelastic Demand
- Unitary Elastic Demand
Table of Content
Let us study these different types of price elasticity of demand.
Perfectly Elastic Demand
Perfectly Elastic Demand Definition: When a small change (rise or fall) in the price results in a large change (fall or rise) in the quantity demanded, it is known as perfectly elastic demand.
Under such type of elasticity of demand, a small rise in price results in a fall in demand to zero, while a small fall in price causes an increase in demand to infinity. In such a case, the demand is perfectly elastic or ep =∞.
Suppose product X is manufactured by a large number of sellers in the market. If a person wants to buy the product X, he could choose among different firms for the purchase. Let’s say, firm A increased the price of product X, above market equilibrium. As a result, the demand for the product X for the firm would decrease to a great extent as the same product is available with other sellers too at cheaper prices. Thus, the demand for product X of the firm A is perfectly elastic.
The extent or degree of elasticity of demand defines the shape and slope of the demand curve. Therefore, the elasticity of demand can be determined by the slope of the demand curve. Flatter the slope of the demand curve, higher the elasticity of demand. In perfectly elastic demand, the demand curve is represented as a horizontal straight line (in parallel to X-axis), which is shown in Figure.
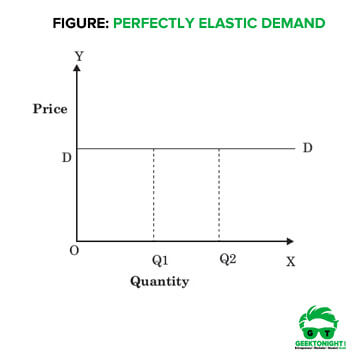
In Figure, DD is the demand curve. Thus, demand rises from OQ to OQ1 and so on, if the price remains at OD. A slight fall in price will increase the demand to OX, whereas a slight rise in price will bring demand to zero.
Let us understand perfectly elastic demand with the help of an example.
Example of perfectly elastic demand
Example: The demand schedule for bread is given below
| Price of Bread (₹ per packet) | Quantity Demanded (per month) |
|---|---|
| 23 | 100 |
| 23.4 | 70 |
Calculate the price elasticity of demand and determine the type of price elasticity.
Solution:
P= 23
Q = 100
P1= 23.04
Q1 =70
Therefore, change in the price of milk is:
ΔP = P1 – P
ΔP = 23.04 – 23
ΔP = 0.04
A change of ₹ 0.04 is a negligible change; thus, can be considered as zero.
Similarly, change in quantity demanded of bread is:
ΔQ = Q1–Q
ΔQ = 70–100
ΔQ = –30
In the above calculation, a change in demand shows a negative sign, which is ignored. This is because price and demand are inversely related which can yield a negative value of demand (or price).
Price elasticity of demand for bread is:
ep = ΔQ/ ΔP × P/ Q
ep = 30/0 × 23/100
ep = ∞
The price elasticity of demand for bread is ∞. Therefore, in such a case, the demand for bread is perfectly elastic.
Perfectly Inelastic Demand
Perfectly Inelastic Demand Definition: When a change (rise or fall) in the price of a product does not bring any change (fall or rise) in the quantity demanded, the demand is called perfectly inelastic demand.
In this case, the elasticity of demand is zero and represented as ep = 0. Graphically, perfectly inelastic demand curve is represented as a vertical straight line (parallel to Y-axis). Figure shows the perfectly inelastic demand curve.
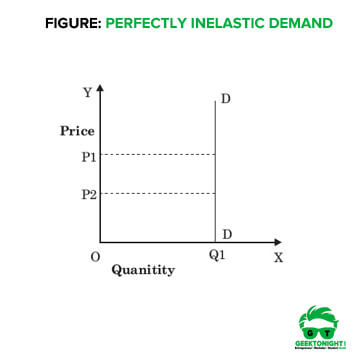
In Figure, DD is the demand curve. Thus, it can be observed that even when there is a change in the price from OP1 to OP2, quantity demanded remains the same at OQ1.
Let us understand perfectly inelastic demand with the help of an example.
Example of Perfectly Inelastic Demand
Example: The demand schedule for notebooks is given below:
| Price of Notebook (₹ per notebook) | Quantity Demanded (per month) |
|---|---|
| 40 | 100 |
| 30 | 100 |
Calculate the price elasticity of demand and determine the type of price elasticity.
Solution:
P= 40
Q = 100
P1= 30
Q1 =100
Therefore, a change in the price of notebooks is:
ΔP = P1 – P
ΔP = 30 – 40
ΔP = –10
In the above calculation, the change in price shows a negative sign, which is ignored. This is because price and demand are inversely related which can yield a negative value of price (or demand).
Similarly, a change in quantity demanded of notebooks is:
ΔQ = Q1 – Q
ΔQ = 100 – 100
ΔQ =0
Price elasticity of demand for notebook is:
ep = ΔQ/ ΔP × P/ Q
ep = 0/10 ×40/100
ep = 0
The price elasticity of demand for notebook is 0. Therefore, in such a case, the demand for a notebook is perfectly inelastic.
Relatively Elastic Demand
Relatively Elastic Demand Definition: When a proportionate or percentage change (fall or rise) in price results in greater than the proportionate or percentage change (rise or fall) in quantity demanded, the demand is said to be relatively elastic demand.
In other words, a change in demand is greater than the change in price. Therefore, in this case, elasticity of demand is greater than 1 and represented as ep > 1. The demand curve of relatively elastic demand is gradually sloping, which is shown in Figure.
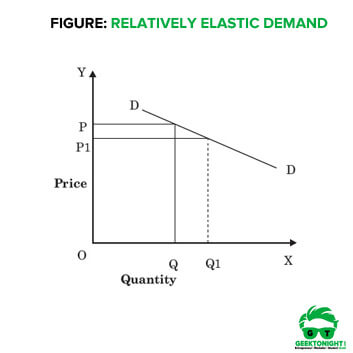
In Figure, DD is the demand curve that slopes gradually down with a fall in price. When price falls from OP to OP1, demand rises from OQ to OQ1. However, the rise in demand QQ1 is greater than the fall in price PP1.
Example of Relatively Elastic Demand
Example: The demand schedule for pens is given below:
| Price of Pen (₹ per pen) | Quantity Demanded |
|---|---|
| 25 | 50 |
| 20 | 100 |
Calculate the price elasticity of demand and determine the type of price elasticity.
Solution:
P= 25
Q = 50
P1= 20
Q1 =100
Therefore, a change in the price of pens is:
ΔP = P1 – P
ΔP = 20– 25
ΔP = – 5
In the above calculation, a change in price shows a negative sign, which is ignored. This is because price and demand are inversely related which can yield a negative value of price (or demand).
Similarly, a change in quantity demanded of pens is:
ΔQ = Q1–Q
ΔQ = 100–50
ΔQ = 50
Price elasticity of demand for pens is:
ep = ΔQ/ ΔP * P/ Q
ep = 50/5 * 25/50
ep = 5
The price elasticity of demand for bread is 5, which is greater than one. Therefore, in such a case, the demand for pens is relatively elastic.
Relatively Inelastic Demand
Relatively Inelastic Demand Definition: When a percentage or proportionate change (fall or rise) in price results in less than the percentage or proportionate change (rise or fall) in demand, the demand is said to be relatively inelastic demand.
In other words, a change in demand is less than the change in price. Therefore, the elasticity of demand is less than 1 and represented as ep < 1. The demand curve of relatively inelastic demand is rapidly sloping, which is shown in Figure.
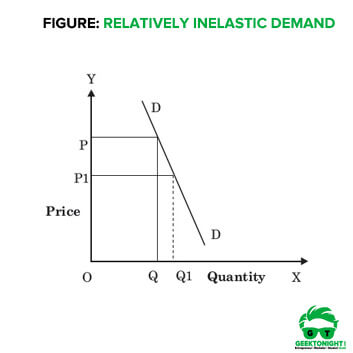
In Figure, DD is the demand curve that slopes steeply with a fall in price. When price falls from OP to OP1, the demand rises from OQ to OQ1. However, the rise in demand QQ1 is less than the fall in price PP1.
Example of Relatively Inelastic Demand
Example: The demand schedule for milk is given below:
| Price of Milk(₹ per litre) | Quantity Demanded |
|---|---|
| 15 | 90 |
| 20 | 85 |
Calculate the price elasticity of demand and determine the type of price elasticity.
Solution: P= 15
Q = 90
P1= 20
Q1 =85
Therefore, a change in the price of milk is:
ΔP = P1 – P
ΔP = 20 – 15
ΔP = 5
Similarly, a change in quantity demanded of milk is:
ΔQ = Q1 – Q
ΔQ = 85 – 90
ΔQ = –5
In the above calculation, a change in demand shows a negative sign, which is ignored. This is because price and demand are inversely related which can yield a negative value of demand (or price).
Price elasticity of demand for milk is:
ep =DQ/DP × P/ Q
ep = 5/5 × 15/90
ep = 0.2
The price elasticity of demand for milk is 0.2, which is less than one. Therefore, in such a case, the demand for milk is relatively inelastic.
Unitary Elastic Demand
Unitary Elastic Demand Definition: Unitary elastic demand occurs when a change (rise or fall) in price results in equivalent change (fall or rise) in demand.
The numerical value for unitary elastic demand is equal to one, i.e., ep =1. The demand curve for unitary elastic demand is a rectangular hyperbola, which is shown in Figure.
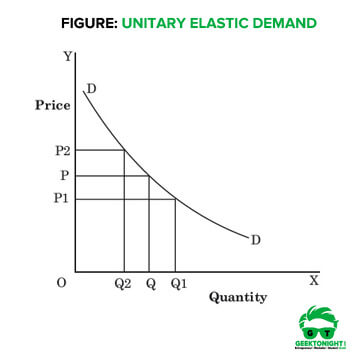
In Figure, DD is the unitary elastic demand curve sloping uniformly from left to the right. Here, the demand falls from OQ to OQ2 when the price rises from OP to OP2. On the contrary, when price falls from OP to OP1, demand rises from OQ to OQ1.
Example of Unitary Elastic Demand
Example: The demand schedule for cloth is given as follows:
| Price of cloth (₹ per litre) | Quantity Demanded |
|---|---|
| 30 | 100 |
| 15 | 150 |
Calculate the price elasticity of demand and determine the type of price elasticity.
Solution:
P= 30
Q = 100
P1 = 15
Q1 = 150
Therefore, change in the price of cloth is:
ΔP = P1 – P
ΔP = 15 – 30
ΔP = –15
In the above calculation, a change in price shows a negative sign, which is ignored. This is because price and demand are inversely related which can yield a negative value of price (or demand).
Similarly, change in quantity demanded of cloth is:
ΔQ = Q1 – Q
ΔQ = 150 –100
ΔQ = 50
Price elasticity of demand for cloth is:
ep = ΔQ/ ΔP × P/ Q
ep = 50/15 × 30/100
ep = 1
The price elasticity of demand for cloth is 1. Therefore, in such a case, the demand for milk is unitary elastic.
Types of Price Elasticity of Demand: Condition
| Numerical Value | Type of Price Elasticity of Demand | Condition |
|---|---|---|
| =∞ | Perfectly elastic demand | Greater change in demand in response to percentage or smaller change in the price. |
| =0 | Perfectly inelastic demand | No change in demand in response to percentage or smaller change in the price. |
| >1 | Relatively elastic demand | A change in demand is greater than the change in price. |
| <1 | Relatively inelastic demand | A change in demand is less than the change in price. |
| =1 | Unitary elastic demand | A change in demand is equivalent to change in price. |
Also Read: Factors Affecting Price Elasticity of Demand
Business Economics Tutorial
(Click on Topic to Read)
Go On, Share article with Friends
Did we miss something in Business Economics Tutorial? Come on! Tell us what you think about our article on Types of Price Elasticity of Demand | Business Economics in the comments section.
Business Economics Tutorial
(Click on Topic to Read)












This was great