What is Measure of Central Tendency?

What is Measure of Central Tendency?

A measure of central tendency is a statistical concept that aims to describe the center or typical value of a dataset. It provides a single value that represents the “middle” or “central” value around which the data tend to cluster. The three most commonly used measures of central tendency are the mean, median, and mode. Measures of central tendency, dispersion and skewness are helpful in analysing numerical data. Let us now study about these measures.

Measures of Central Tendency

A measure of central tendency is a precis statistic that represents the middle factor or regular price of a dataset. These measures imply wherein maximum values in a distribution fall and also are called the central area of distribution. You can think about it because of the tendency of statistics to cluster around a centre price. The measures of central tendency are used to study the distribution pattern of a dataset. These measures give a central value that represents the large chunk of data analysed. The central value is nothing but the average of data collected.

Mean

Mean represents the value calculated after dividing the sum of observations by the total number of observations (n) taken. It is also known as arithmetic mean.

The following formula is used to calculate mean:

Let us understand the concept of arithmetic mean with the help of an example. Suppose you want to find the average weight of a group of five friends. Table 8.1 shows the weight of each person in the group:

People	Weight (kg)
Jenny	35
Robert	40
Ella	34
Andy	39
Eliza	42

The average weight of five friends can be calculated as follows:

X = ∑Xi
/n
Where, X = Average weight of five friends
∑Xi
= Sum of the weights of five friends
∑Xi
= 190
n = 5
X = (35 + 40 + 34 + 39 + 42)/5
X = 190/5
X = 38 kg

Therefore, the average weight of five friends is 38 kg.

You can calculate different types of mean:

Weighted Mean

This mean is calculated after considering the weight attached to each item. The formula used to calculate weighted mean is as follows:

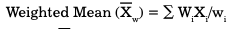
Where, Xw = Symbol for weighted mean
Xi = Value of the ith item
Wi = Weight assigned to the ith item
wi = Number of weights assigned

Example of Weighted Mean

A school grades its students by using weighted mean scores as follows: 15% weightage is assigned for homework, 15% weightage is assigned for extracurricular activities, and 70% weightage is assigned for the examination. Aditya scored 60 marks, 70 marks and 55 marks for homework, extracurricular activities and in examination respectively. Find the weighted score of Aditya if the total score is 100.

Now, you calculate the weighted mean as follows:

Weighted Mean (Xw) = (0.15 × 60) + (0.15 × 70) + (0.70 × 55)
= 9 + 10.5 + 38.5
= 58

Geometric Mean

Geometric mean represents the nth root of the product of all the values or observations involved in a research. The formula used to calculate geometric mean is as follows:

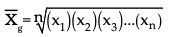
Where X₁ , X₂…………,X_n are the n observations in the data set

n = Number of observations

Example of Geometric Mean

You want to calculate the geometric mean of four observations: 10, 12, 10 and 11.

The calculation of geometric mean is shown as follows:

X₁ = 10, X₂ = 12, X₃ = 10, X₄ = 11

n = 4

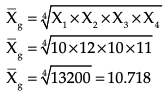
Therefore, the geometric mean of four observations is 10.7 years.

Harmonic Mean

Harmonic mean refers to reciprocal of the average of the reciprocals of the values in a data series (or observations). The formula to calculate harmonic mean is as follows:

Harmonic mean (XH) = Rec. [(Rec. X1 + Rec. X2 +…………. + Rec. Xn)/n]

Where Rec. X₁ , Rec. X₂ …. Rec. X_n are the Reciprocal of Observations 1, 2, ….., n, respectively

n = Number of observations

Example of Harmonic Mean

Calculate the harmonic mean of four observations: 10, 12, 10 and 11.

Harmonic mean is calculated as:

(XH) = Rec. [(Rec. X1 + Rec. X2 + …………. + Rec. X4 )/n]

Where Rec. X₁ = 1/10; Rec. X₂ = 1/12, Rec. X₃ = 1/10; Rec. X₄ = 1/11

n = 4

Therefore, the harmonic mean of the four observations is 10.7 years. It is used for units that add up as reciprocals in a sequence such as speed, distance, capacitance in series or resistance in parallel.

Median

Median is defined as a central or mid value of a dataset. Median divides a dataset into two halves – one half contains the values greater than the mid value (or median) and the other half contains the values less than the mid value. Before calculating median, you need to arrange the dataset in the ascending or descending order. The formula to calculate median is as follows:

n = number of observation

Now, if n is an odd number

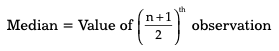
Now, If n is an even number

Median = Value of {[(n/2)^th observation + ((n+1)/2)^th ]/2}

Let us understand the concept of median with the help of an example.

A group of 17 people gave the following ratings to a book on a 5-pointer scale (where 1 is the lowest rating and 5 is the highest rating):

2, 5, 3, 4, 1, 5, 4, 3, 1, 2, 5, 4, 3, 2, 1, 5, 4

Now you want to calculate the average rating by using median. To do so, arrange the data in the ascending order, as follows:

1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5

Since the number of observations is odd, the following formula will be used to calculate median

Median = Value of ((n + 1)/2)^th observation

Median = ((17 + 1)/2)^th observation

Median = 9^th observation

Median = 3

Therefore, the median rating for the book is 3.

Now, if n is an even number; then, we calculate median as the simple average of the middle two numbers. In other words, median is the simple average of the (n/2)th and ((n +1)/2 )th terms.

Now, if a group of 20 people gave their ratings to a movie on a 5-point scale as:

2, 5, 3, 4, 1, 5, 4, 3, 1, 2, 5, 4, 3, 2, 1, 5, 4, 1, 2, 3

Where, 1 is the lowest rating and 5 is the highest rating

Now, to calculate the average rating using median, all the 20 observations are arranged in ascending order as:

1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5

Here, median is the average of middle two values, i.e., values at 10th and 11th positions. This is calculated as:

Median = (3 + 3)/2 = 3

Mode

Mode refers to the value that has the highest frequency in a data series. According to Croxton and Cowden, the mode of a distribution is value at the point around which the items tend to be most heavily concentrated. It may be regarded as the most typical of a series of values. Let us learn to calculate mode with the help of an example. Suppose the marks of five friends in a science paper are 70, 90, 50, 70, and 30. You want to find the mode of their marks.

You need to find the highest frequency of the present data to calculate mode. Here, the number having the highest frequency is 70 as it occurs two times; therefore, the mode of students’ marks is 70. Mode is used as the most important statistic for nominal data where values are names rather than numbers. In such cases, there is no concept of centre because there are no numbers. In addition, when we are dealing with continuous variables, probability that observations occurring in the data sample are different is 1. Therefore, mode cannot be used for continuous variables.

Mode is not considered a true measure of central tendency because of three reasons:

• It is not necessary that one data series has only one mode because many numbers in the data series can have the highest frequency.
  
  
• Mode does not consider all the frequencies to arrive at the central value of the data series. Therefore, the results of mode are not reliable.
  
  
• It is possible that a series has observations that occur only once. In such cases, mode does not exist.

Let us summarise mean, median and mode as:

• Mean: Mean represents the average value in a dataset.
• Median: Median represents the middle value in a dataset.
• Mode: Mode represents the most common value in a dataset.