What is Capital Assets Pricing Model (CAPM)? Assumptions, Inputs

What is Capital Assets Pricing Model (CAPM)?

Capital Asset Pricing Model (CAPM) is a financial model used to rate risky securities, which explain the link between risk and anticipated return. It ascertains what the rate of return of an asset is going to be, presuming that it is to be included to a well-diversified portfolio, granted that asset’s systematic risk.

The model was introduced by Jack Treynor, William Sharpe, John Lintner and Jan Mossin independently, building on the earlier work of Harry Markowitz on diversification and modern portfolio theory.

The CAPM is a model for pricing an individual security or a portfolio. The CAPM, in essence, predicts the relationship of an assets and its expected return. This relationship helps in evaluating various investments options. The CAPM assumes that investors hold fully diversified portfolios.

The measure of risk used in the CAPM, which is called ‘beta’, is therefore a measure of systematic risk.

The minimum level of return required by investors occurs when the actual return is the same as the expected return, so that there is no risk at all of the return on the investment being different from the expected return. This minimum level of return is called the ‘risk-free rate of return‘

Therefore, the expected rate of return for any security under CAPM is deflated by the following equation:

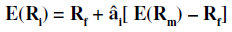
Where:
E (Ri) = Return required on financial asset i
Rf = Risk-free rate of return
âi = Beta value for financial asset i
E (Rm) = Average return on the capital market

---

Assumptions of CAPM

The CAPM is often criticized as being unrealistic because of the assumptions on which it is based, so it is important to be aware of these assumptions and the reasons why they are criticized. The assumptions are as follows:

• Investors hold diversified portfolios: This assumption means that investors will only require a return for the systematic risk of their portfolios since unsystematic risk has been eliminated and can be ignored.
  
  
• Single-period transaction horizon: A standardized holding period is assumed by the CAPM in order to make comparable the returns on different securities. A return over six months, for example, cannot be compared to a return over 12 months. A holding period of one year is usually used.
  
  
• Investors can borrow and lend at the risk-free rate of return: This is an assumption made by portfolio theory from which the CAPM was developed, and provides a minimum level of return required by investors.
  
  
• Perfect capital market: This assumption means that all securities are valued correctly and prices reflect all information.
  
  
• Homogeneous expectations: All investors analyze securities in the same way and share the same economic view of the world. The result is identical estimates of the probability distribution of future cash flows from investing in the available securities.
  
  
• Rational Investors: All investors are rational mean-variance optimizers. It means that at a given level of risk they want to maximize their return and for a given level of return they want to minimize their risk.

---

Inputs for CAPM

To apply the CAPM, you need to estimate the following factors:

• Risk-free rate of return
• Market risk premium
• Beta

Risk Free rate of Return

In theory, the risk-free rate is the minimum rate of return an investor expects for any investment with zero risk. In practice, however, the risk-free rate does not exist because even the safest investments carry a very small amount of risk.

However, short-term government debt is a relatively safe investment and in practice, return on these assets can be used as an acceptable proxy for the risk-free rate of return under CAPM. The risk-free rate of return is also not fixed, but will change with changing economic circumstances.

Market Risk Premium

Market risk premium is the difference between the expected return on a market portfolio and the risk-free rate. It results of investment in risky security rather than risk-free security. The market risk premium can be calculated as follows:

Market Risk Premium = Expected Return of the Market – Risk Free Rate

Beta

Beta is an indirect measure which compares the systematic risk associated with a company’s shares with the systematic risk of the capital market as a whole. If the beta value of a company’s shares is 1, the systematic risk associated with the shares is the same as the systematic risk of the capital market as a whole.

Beta can also be described as ‘an index of responsiveness of the returns on a company’s shares compared to the returns on the market as a whole’.

For example, if a share has a beta value of 1, the return on the share will increase by 10% if the return on the capital market as a whole increase by 10%. If a share has a beta value of 0.5, the return on the share will increase by 5% if the return on the capital market increases by 10%, and so on. Beta values are found by using regression analysis to compare the returns on a share with the returns on the capital market.

Beta can be calculated as fallow:

Beta = Cov (Ri,Rm)/Variance of Rm

Where:
Cov (Ri,Rm) = Covariance between individual security and market return
Ri= Individual security return
Rm= Market return

---

Security Market Line (SML)

The security market line (SML) is the line that reflects an investment’s risk versus its return, or the return on a given investment in relation to risk. The measure of risk used for the security market line is beta.

The SML essentially graphs the results from the capital asset pricing model (CAPM) formula. The x-axis represents the risk (beta), and the y-axis represents the expected return.

The market risk premium is determined from the slope of the SML. The relationship between â and required return is plotted on the securities market line (SML) which shows expected return as a function of â.

The intercept is the nominal risk-free rate available for the market, while the slope is the market premium, E (Rm) ?Rf. The securities market line can be regarded as representing a singlefactor model of the asset price, where beta is exposure to changes in value of the Market. The equation of the SML is thus:

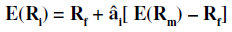
Where:
E (Ri) = Return required on financial asset i
Rf = Risk-free rate of return
âi = Beta value for financial asset i
E(Rm) = Average return on the capital market

---

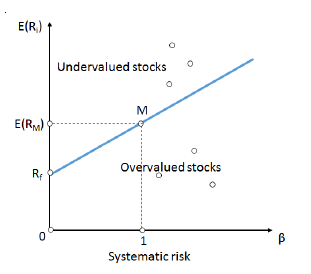
Capital Market Line (CML)

As discussed in the previous section, adjusting for the risk of an asset using the riskfree rate, an investor can easily alter his risk profile. Keeping that in mind, in the context of the capital market line (CML), the market portfolio consists of the combination of all risky assets and the risk-free asset, using market value of the assets to determine the weights.

The CML defined by every combination of the risk-free asset and the market portfolio. The Mean-Variance criteria as proposed by Henry Markowitz’ did not take into account the risk-free asset.

The CML results from the combination of the market portfolio and the riskfree asset. All points along the CML have superior risk-return profiles to any portfolio on the efficient frontier, with the exception of the Market Portfolio, the point on the efficient frontier to which the CML is the tangent.

From a CML perspective, this portfolio is composed entirely of the risky asset, the market, and has no holding of the risk free asset, i.e., money is neither invested in, nor borrowed from the money market account.

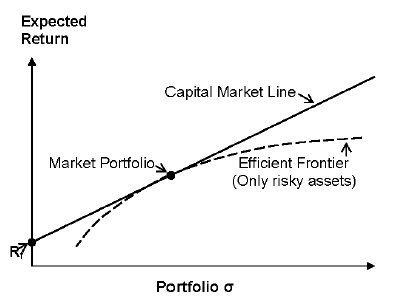
Where:
E(Ri)= Expected rate of return of portfolio (i)
Rf = Risk free rate of return
λ= slope of CML
σ = standard deviation of portfolio (i)

The slope of CML can be obtained as follow:

λ=E(Rm) – Rf/ σ

λ= Slope of capital market line
σ = standard deviation of market returns