What is Forward Rate Agreements (FRAs)?
Forward Rate Agreements (FRAs) are derivative products used for hedging against interest rate uncertainty by banks and corporates. They are not exchange-traded derivative products but are like foreign exchange forward contracts, tailor-made to suit the needs of counterparties, traded in the OTC market.
An FRA is defined as a financial contract between two parties to exchange interest payments for a ‘notional principal’ amount on settlement date, for a specified period from start date to maturity date. Accordingly, on the settlement date, cash payments based on contract (fixed) and the settlement rate are made by the parties to one another. The settlement rate is the agreed benchmark/ reference rate prevailing on the settlement date (RBI, 1999).
Table of Content
From the above definition, the salient features of an FRA can be derived as follows:
- It involves only an exchange of interest payments on a notional principal amount. There is no exchange of principal.
- It involves the exchange of interest applicable for one specific future period.
- The exchange is between a contracted interest rate, agreed to in advance, and an interest rate to be determined later, based on agreed benchmark reference rates like LIBOR, EURIBOR, etc.
- The settlement-floating rate is a benchmark rate on the agreed settlement date. As you will see later, the term settlement date has a different meaning in the case of FRA.
In an FRA, two parties contract on the interest rate applicable for a certain future period. One who purchases the FRA (“long on FRA”) contracts to pay at a specified fixed interest rate, agreed in advance, on a notional principal, and receive floating interest rate to be determined on the settlement date. The settlement of the payment under the FRA contract is done on the settlement date based on the difference between the interest rate contracted and the benchmark interest rate applicable for the future period.
Consider a bank that plans to borrow in interbank LIBOR markets after three months. The loan tenor is for six months. Let us say the current LIBOR for six months is 5%. However, the six-month LIBOR applicable after three months could increase to 7%. Thus, the bank faces uncertainty with regard to the amount of interest it has to pay when it actually borrows after three months. It would like to fix the interest it needs to pay on the future loan now itself. Another bank might have a need to invest after three months for a six-month duration.
It faces the risk that the six-month LIBOR could fall down to 4% after three months. It would like to fix the interest it would receive on its future investment. The two banks can hedge their risks by entering into a forward rate agreement. Bank A will contract to pay 5% to Bank B and receive whatever six-month LIBOR prevailing after three months (i.e., settlement date). Bank A will borrow after three months at the six-month LIBOR and will use the LIBOR interest received from Bank B for paying off the loan interest.
Bank B will invest at whatever six-month LIBOR prevailing after three months and pay the LIBOR interest received from the investment to Bank A and receive 5% in lieu of it. Thus, Bank B has also fixed its interest income by entering into the contract. Both the banks have thus eliminated their interest rate uncertainties. The above contract is called FRA and Bank A, which pays fixed interest, is called the FRA buyer, and Bank B, which pays floating rate interest, is called the FRA seller. An important aspect of an FRA contract is that two banks need not wait for the end of six months to exchange the interest payments (i.e., nine months from now).
Since both the interest rates will be known after three months itself, instead of waiting until nine months, they can exchange the present value of the difference between the two interest payments discounted for six months at the settlement date after three months. Such an FRA contract is termed “3 × 9”, which means that it involves the exchange of six-month interest applicable after three months. FRAs are used by banks for hedging interest rate risks arising out of asset-liability mismatches and by corporates for locking in a future interest rate.
Suppose a bank has an asset maturing after six months, while the corresponding liability is maturing after nine months. The asset has to be reinvested after six months for another three months in order to use it for paying off the maturating liability at nine months from now. If the asset has been placed at the contracted interest rate for nine months (instead of six months), the maturity amount would have matched the liability exactly. However, the bank now has to reinvest after six months in a three-month instrument whose interest could be anything after six months.
To illustrate, the bank has a payment to be made in US dollars for 10.25 million after nine months. It faces exchange rate risk unless otherwise the above liability is matched with a nine-month asset maturing for $10.25 million. Assume that the bank also has an asset in US dollars maturing after six months for $10 million. On maturity, the bank can reinvest this $10 million for three months so that the maturing amount can be used to payoff the liability. The current interest rate for threemonth deposit is 10% p.a. If the interest rate remains the same at 10% p.a. after six months for three-month deposit, the bank will realise $10.25 million after nine months.
However, it is quite possible that the interest rate could come down. Thus, the bank faces exchange rate risk arising out of asset-liability mismatch. Similar to currency forward contracts, if the bank can fix the three-month interest rate, applicable after six months, it can eliminate the exchange rate risk. FRAs enable banks to do exactly that. Assume now a corporate that has a USD borrowing maturing after six months, which it needs to rollover for another three months. It is worried that the three-month interest rate applicable after six months could be more than currently quoting 10% p.a. It faces the interest rate risk similar to the bank’s above.
The bank and the corporate can enter into an FRA contract to hedge their respective interest rate risks. The bank wants the three-month interest rate to be above 10%, while the corporate wants it to be below 10%. Both of them can enter into a forward contract at an interest rate of 10%. The contract should be such that if the interest rate is higher than 10%, the bank loses from FRA and the corporate gains. Since FRA is a hedge for the borrowing of the corporate, gains in FRA will be offset by a higher interest rate (that the corporate will pay on its future borrowings).
If the interest rate is less than 10%, the bank will benefit, as FRA gains will offset the lower maturity amount of the asset to be invested after three months. The FRA terminology is that the buyer of an FRA is one who will benefit if the actual interest rate turns out to be higher (long on FRA or borrower). The seller of an FRA is the counterparty who will benefit if the interest rate goes down (short on FRA or lender). In the above case, the bank will be the seller of the FRA and the corporate will be the buyer.
FRA Settlement
FRA settlement is done based on the present value of the interest rate difference on the notional principal. Suppose the bank sells the above FRA at 10% p.a. to the corporate. After six months, if the three-month interest rate turns out to be 6% p.a., the buyer of FRA, the corporate, loses, while the bank gains. The corporate contracted FRA at 10% p.a. but the three-month rate is now 6% p.a. Hence, it has to pay the present value of difference to the bank. The settlement is on the basis of the present value of difference since FRAs originated in interbank deposit markets where the FRA writer/seller is assumed to buy a deposit on the maturity date at the contracted rate. Instead of making the actual deposit, the present value of difference is settled.
The amount to be settled is calculated as follows:
Amount to be settled = Present value of (Maturity amount at 10% p.a. – Maturity amount applicable if 6% p.a.)
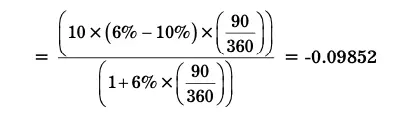
The corporate has to pay $ 0.09852 million to the bank.
You can verify the hedge as follows:
If the bank has not sold FRA, it will earn only 6% on the $ 10 million deposit made after six months, i.e., a maturity amount of $0.15 million after nine months. However, it should earn an interest amount of $0.25 million in order to meet the liability of $10.25 million. The difference is a deficiency of $0.1 million. Its present value is $0.9852 million after six months. This is exactly the gain it makes in FRA transaction.
Similarly, the corporate gains because the interest rate itself turns out to be 6% while it locked in a rate of 10%. Hence, it pays the present value of the difference amount of 4% to the bank. Effectively, the corporate’s interest cost is 10%, while the bank is able to earn 10% on its three-month deposit to bridge the asset-liability gap.
FRA Market Conventions
FRAs are OTC products that are not traded in derivative exchanges. These are like forward contracts on currencies that are entered either between banks or between banks and corporates. FRAs are generally traded on the basis of LIBOR as the reference rate in the London eurodollar interbank markets. As mentioned before, the FRA contract is generally referred to in short notation by terms like “6×9”.
It means “six month forward three-month LIBOR” where six refers to settlement after six months and nine refers to the maturity date of FRA (or maturity of notional deposit) being after nine months. The FRA rate quoted for such a contract is the rate applicable for a three-month deposit to be placed after six months. Similarly, an FRA quote for “3×9” implies the FRA rate applicable for six- month deposit to be placed after three months. The formula for the settlement amount (i.e., profit or loss) for an FRA of “n × m r%” can be given as follows:
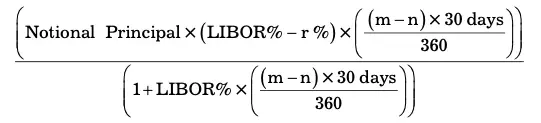
Where LIBOR is the actual LIBOR applicable for (m-n) months after n months and r is the forward rate contracted. The term 360 is the days count convention for a year in LIBOR markets. It depends on market conventions applicable for each market. In the example above, you assumed 10% interest rate as the rate that two parties wanted to lock in for a three-month period applicable after six months. In practice, this will be the rate extracted from the yield curve (i.e., interest rate applicable for a three-month deposit after six months as per the current yield curve). This concept will be clear with the hedging example explained below.
Pricing and Hedging an FRA Contract
In the example discussed above, the bank had an exposure to interest rate risk that mirrored exactly the hedging requirement of the corporate. However, banks, being market makers in the FRA market, need not have exact opposite exposure to provide an FRA facility to corporates. Banks can tailor an FRA contract as per the needs of corporates and then hedge the same with money market operations. For example, in the previous example, if the bank did not have any asset-liability gap, it could still offer an FRA facility to the corporate and then hedge the same by creating the same asset-liability pattern.
It would involve the following steps:
- Borrow US dollars for nine months such that the maturity amount is $10 million after six months.
- Deposit the amount borrowed for six months to be rolled over for another three months at the FRA rate.
The above asset-liability pattern is the same with which we explained FRA earlier.
Example Below Explain It Further
Example: A bank sells a 3×6 FRA for GBP 100 million to a corporate.
The three-month LIBOR interest rates are quoted at 4.40% / 4.45%.
The six-month LIBOR interest rates are quoted at 4.81% / 4.87%.
- What should be the FRA quoted by the bank?
- How the bank will hedge this FRA exposure?
- Explain how the hedge can be useful in different interest scenarios.
Solution: A 3×6 FRA quote is the interest rate applicable for a threemonth deposit placed after three months. This rate can be derived from the relevant part of the yield curve. The rates as per the LIBOR yield curve are given. These rates are given in terms of bid/offer rates. The bank is a seller in the FRA, which means it will benefit from a fall in interest rates. It also means the bank is willing to accept a threemonth GBP 100 million deposit at the FRA rate after three months. The bank is locking in the FRA rate as the interest it needs to pay on that deposit.
It will lend this deposit at the prevailing interest rate after three months. If the interest rate goes down, the loss due to a higher interest rate on the deposit will be compensated by FRA gains. If the interest rate goes up, the bank will lose on the FRA, which will be compensated by the lower interest rate on the deposit contracted. FRA works on the notional principal and only settlement on interest difference will be done. Hence, the bank has to hedge the above asset-liability pattern with money market operation. Basically, the bank should hedge the FRA rate through money market transactions.
This can be achieved through the following transactions:
- Borrow for six months.
- Place borrowed funds on deposit for three months.
- After three months, roll-over the deposit for another three months at market rates.
- Close the loan with proceeds of the deposit after six months. The difference in maturity proceeds will be compensated by FRA gains/losses.
By taking a six-month loan and placing it for a three-month deposit, the three-month interest rate applicable after three months implied in the LIBOR yield curve gets locked. To mathematically express this fact:
(1+3-month interest of period 1) × (1+ 3-month interest of period 2) = (1+ 6-month interest)
In other words, as per the yield curve, in order to prevent arbitrage opportunities, a six-month instrument should give the same return as compared to a three-month instrument rolled over after three months for another three months.
The “three month interest of period 2” is the FRA rate to be quoted by the bank.
The borrowing for six months will be done at the offer rate of 4.87% p.a.
The borrowed funds will be placed on three-month deposit at the bid rate of 4.4% p.a.
(1+ 4.40% × 3/12) × (1+ FRA × 3/12) = (1+ 4.87% × 6/12)
From the above equation, we can derive the FRA rate as 5.2819% p.a.
The bank will quote at a spread over the above rate.
For hedging, the bank will have to borrow such that the maturity amount is GBP 100 million after three months.
Amount to be borrowed at 4.87% = 100 / (1+4.4% ×3/12) = GBP 98.91197 million
The bank will place GBP 98.91197 million as a three-month deposit at 4.4%. It will rollover the deposit for another three months at the future interest rate.
Hedge Verification:
(Assume FRA rate is 5.6849%)
Case (a) – Interest rate for three-month deposit after three month 6% p.a.
The maturity amount of the deposit of borrowed funds after three months = GBP 100 million
This amount will be rolled over at 6% for three months.
The maturity amount after six months = 100 × (1+6% × 3/12) = 101.5
The maturity amount for loan repayment = 98.91197 × (1+ 4.87% × 6/12) = 101.3205
Thus, due to increase in interest rates, the maturity amount of the deposit is more at 101.5 as compared to loan repayment requirement of 101.3205. There is a gain of 0.18 million.
However, since the bank is the seller and the interest rates have gone up, the bank will lose on FRA. The FRA settlement amount can be calculated as follows:
Notional profit or lossfor the buyer= 0.1769
The bank has to pay to the FRA buyer GBP 0.1769 million on the settlement date. This amount is the same as the present value of the gain made in the money market hedge. You can verify that the present value of 0.18 gains at 6% is same as the above amount.
Thus, FRA has been hedged with the money market lending/borrowing.
Case (b) – Interest rate for three-month deposit after three month 3% p.a.
This amount will be rolled over at 3% for three months.
The maturity amount after six months = 100 × (1+3% × 3/12) = 100.75.
The maturity amount for loan repayment = 98.91197 × (1+ 4.87% × 6/12) = 101.3205
Thus, due to decrease in interest rates, the maturity amount of the deposit is less at 100.75 as compared to the loan repayment requirement of 101.3205. There is a deficiency of 0.5705 million. You can verify that this amount will be compensated from the gain in FRA transaction.
Since the bank is the seller and interest rates have come down, the bank will gain on the FRA. The FRA settlement amount can be calculated as follows:\
Notional profit or lossfor the buyer=

The bank will receive from the FRA buyer GBP 0.56623 million on the settlement date.
The maturity value of this FRA gain after three months = 0.56623 × (1+3% × 3/12) = 0.5705
This amount is the same as the deficiency in the loan repayment amount available in the money market hedge.
Thus, FRA has been fully hedged with money market transactions in either of the scenarios.




