Rat and Poison Puzzle
You have 1000 wine bottles, one of which is poisoned. You want to determine which bottle is poisoned by feeding the wine to the rats. You have 10 rats to test on to find out which bottle is deadly. The poison takes effect after an hour of consumption, so you only have one chance to run your rat poison experiment
Solution:
#1 Label Rat and Poison Bottle
First, let’s line up our 10 rats and label them. Also, label the wine bottles 0–1000 so we can tell them apart.
These rats will represent the digits of a binary number. So the rightmost rat represents the ones. Then the next one over is the twos, then the fours, and so on. The left-most rat represents the 512th place.
Also, label each bottle with both its decimal number and binary equivalent.
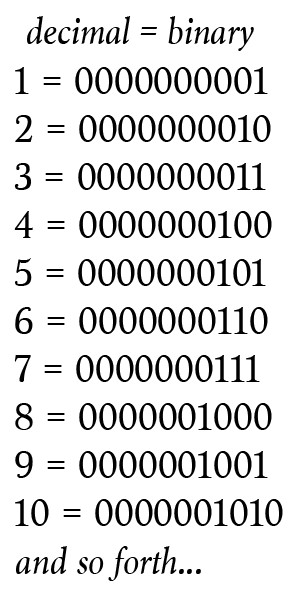
Pretty clever, isn’t it? Because there are 10 rat and each prisoner has two states (dead or alive), this system has a grand total of 1,024 different combinations.
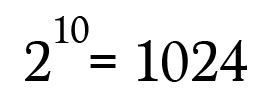
This is more than enough combinations since we only have 1000 bottles.
The bottle assignments reflect the powers of 2.
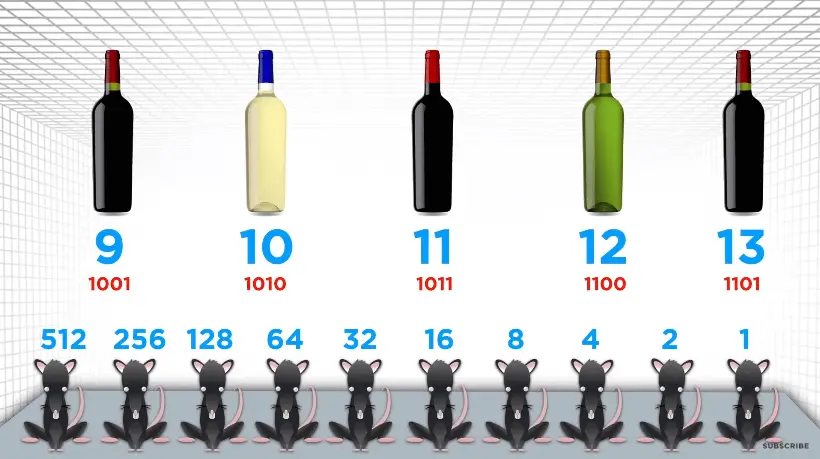
Take each bottle of wine, and feed it to those rats which represent a one in the binary number on the bottle’s label.
#2 Example: Rat and Poison
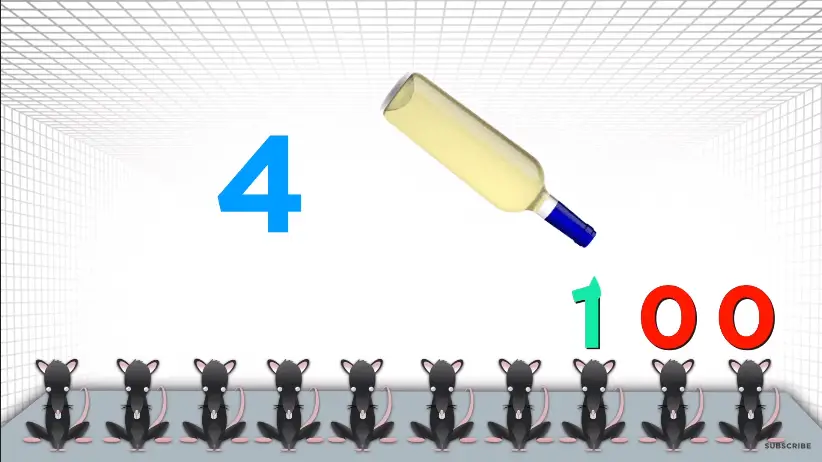
Bottle number 4 is 1 0 0 in binary. So feed one drop of bottle 4 to the third rat from the right.
Bottle number 295 is represented in binary as 1 0 0 1 0 0 1 1 1, so feed it to these corresponding rats.

After you’ve given a few drops of wine to the appropriate rats, wait an hour. Now, how can you tell exactly which bottle is poisoned?
This is the part that’s so amazing. You can just read the number for the poisonous bottle from the rats. You have a line of rats, some dead and some alive.
Just imagine all the dead rats are ones, and all the alive rats are zeros. This gives a 10 digit string of zeros and ones.
You know that the poisonous bottle is 1 1 0 1 0 1, or as it’s more commonly referred to in base 10, number 53, and the party is saved.

Image Source: PBS Infinity Series
Go On, Challenge this Puzzle to your Friends!
Did we miss something in Puzzle Interview Series? Come on! Write comments if you find anything incorrect, or you want to share more information about our puzzle for interview on Rat and Poison Puzzle 1 | Puzzle Interview



